| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
Tags
- 미쉬킨의화폐와금융 #미쉬킨 #화폐금융론 #화폐와금융 #경제학 #교양 #경제지식 #경제공부
- 블록체인 #layer2 #레이어2 #이더리움스케일링
- 자료구조 #알고리즘
- #국제채권시장 #유로본드 #유로커런시 #유로달러 #외국채 #금융중개기관 #간접금융 #거래비용#다우존스공업평균지수 #나스닥종합지수 #FTSE100 #DAX #CAC40 #straittimes #항생지수 #거래비용 #유동성 #위
- #경제상식 #화폐 #금융 #화폐금융론 #경제학 #경제기본 #경제지식 #경제근육 #투자지식 #경제공부 #경제학전공 #금융이란 #화폐란 #금융시장 #금융시장역할 #화폐역할 #화폐역기능 #금융역기능 #
- vp #vc #did #신원인증 #블록체인
- 페이스북유니버시티 #마케팅교육 #마케팅캠프
- html #js #parsing
Archives
- Today
- Total
평행우주 : world 1
[Algorithm] 시간 복잡도 개념 정리 본문


시간 복잡도
- 입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마만큼 걸리는가?를 고려
- 주로 빅-오 표기법을 사용해 나타낸다
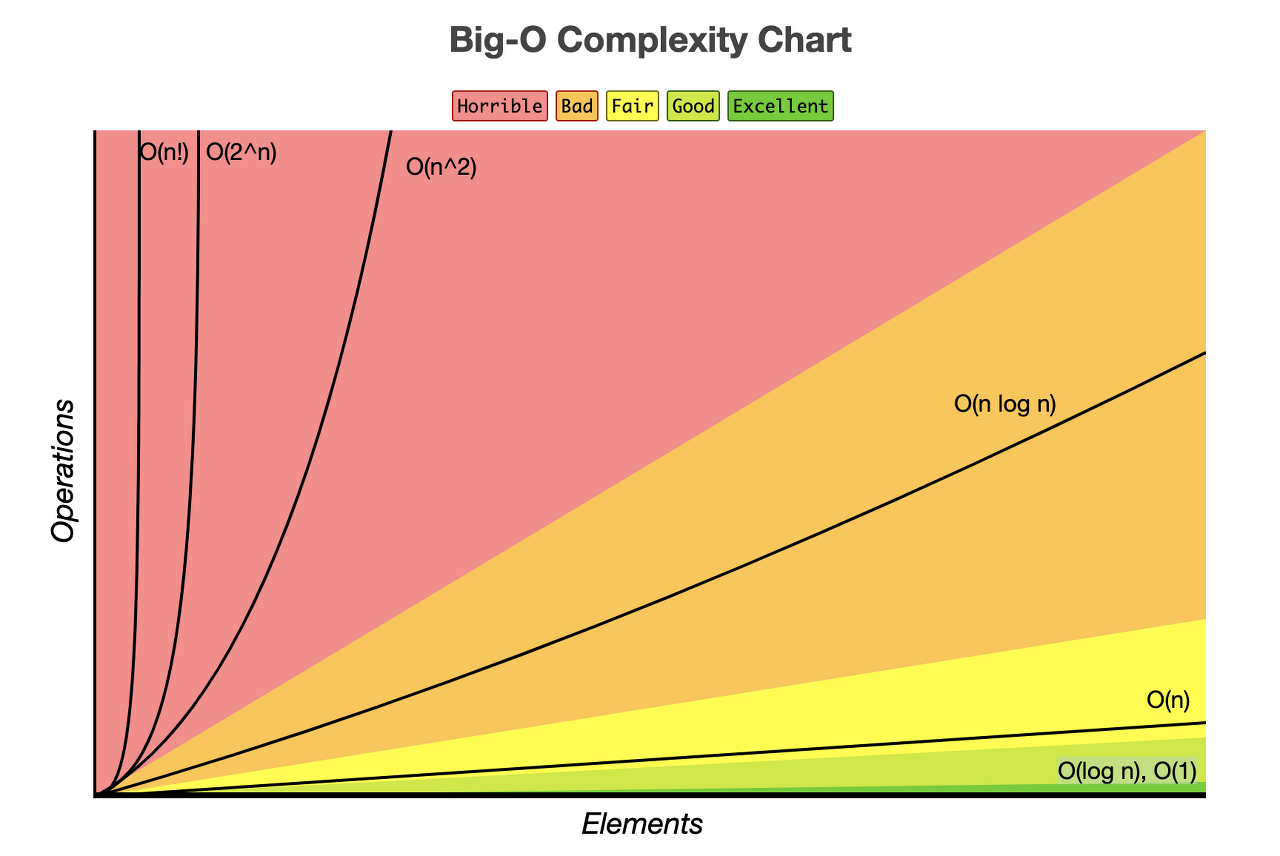
Big-O 표기법
- 빅오 표기법은 최악의 경우를 고려
- 프로그램이 실행되는 과정에서 소요되는 최악의 시간까지 고려할 수 있다.
- "최소한 특정 시간 이상이 걸린다" 혹은 "이 정도 시간이 걸린다"를 고려하는 것보다 "이 정도 시간까지 걸릴 수 있다"를 고려
- 최악의 경우도 고려하여 대비하는 것이 바람직하기 때문에 다른 표기법보다 Big-O 표기법을 많이 사용
+)
시간 복잡도를 각각 최악, 최선, 중간(평균)의 경우에 대하여 나타내는 방법
- Big-O(빅-오)
- Big-Ω(빅-오메가)
- Big-θ(빅-세타)
O(1) : constant complexity
- 입력값이 증가하더라도 시간이 늘어나지 않음
- 즉, 입력값의 크기와 관계없이, 즉시 출력값을 얻어낼 수 있다

O(1)의 시간 복잡도를 가진 알고리즘
//arr의 길이가 100만이라도, 즉시 해당 index에 접근해 값을 반환할 수 있다.
function O_1_algorithm(arr, index) {
return arr[index];
}
let arr = [1, 2, 3, 4, 5];
let index = 1;
let result = O_1_algorithm(arr, index);
console.log(result); // 2
O(n) : linear complexity
- 입력값이 증가함에 따라 시간 또한 같은 비율로 증가.
- 입력값이 1일 때 1초의 시간이 걸리고, 입력값을 100배로 증가시켰을 때 1초의 100배인 100초가 걸리는 알고리즘

O(n)의 시간 복잡도를 가진 알고리즘
//입력값(n)이 1 증가할 때마다 코드의 실행 시간이 1초씩 증가합니다.
//즉 입력값이 증가함에 따라 같은 비율로 걸리는 시간이 늘어난다.
function O_n_algorithm(n) {
for (let i = 0; i < n; i++) {
// do something for 1 second
}
}
//입력값이 1 증가할때마다 코드의 실행 시간이 2초씩 증가
//O(2n) 이지만,입력값이 커지면 커질수록 계수의 의미가 점점 퇴색되기 때문에
//같은 비율로 증가한다면, O(n)으로 표기
function another_O_n_algorithm(n) {
for (let i = 0; i < 2n; i++) {
// do something for 1 second
}
}
O(log n) : logarithmic complexity
- Big-O표기법중 O(1) 다음으로 빠른 시간 복잡도
- 매번 숫자를 제시할 때마다 경우의 수가 절반이 줄어든다
- BST의 값 탐색도 같은 로직으로 O(log n)의 시간 복잡도를 가진 알고리즘(탐색기법)
- 1~100 중 하나의 숫자를 플레이어1이 고른다 (30을 골랐다고 가정).
- 50(가운데) 숫자를 제시하면 50보다 작으므로 down을 외친다.
- 1~50중의 하나의 숫자이므로 또다시 경우의 수를 절반으로 줄이기 위해 25를 제시한다.
- 25보다 크므로 up을 외친다.
- 경우의 수를 계속 절반으로 줄여나가며 정답을 찾는다.

O(n2) : quadratic complexity
- 입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가
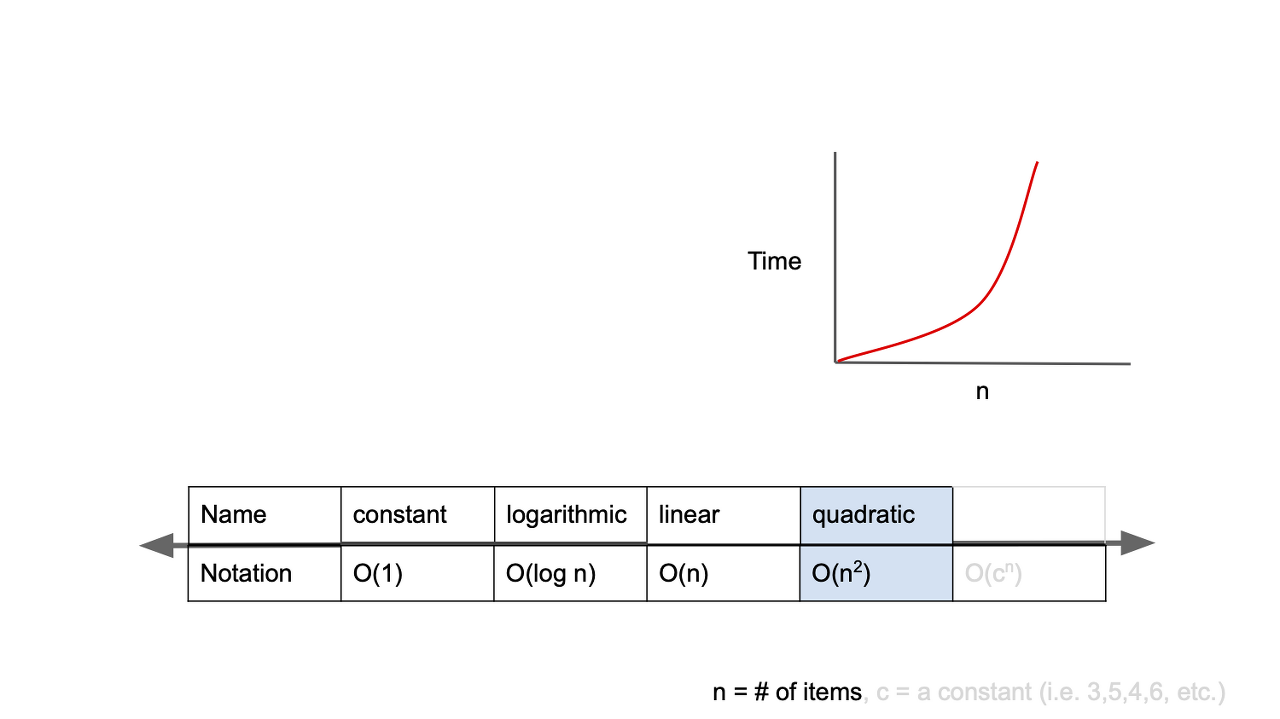
O(n2)의 시간 복잡도를 가지는 알고리즘 예시
function O_quadratic_algorithm(n) {
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
// do something for 1 second
}
}
}
function another_O_quadratic_algorithm(n) {
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
for (let k = 0; k < n; k++) {
// do something for 1 second
}
}
}
}
O(2n) : exponential complexity
- Big-O 표기법 중 가장 느린 시간 복잡도

O(2n)의 시간 복잡도를 가지는 알고리즘 예시
//재귀로 구현하는 피보나치 수열은 O(2n)의 시간 복잡도를 가진 대표적인 알고리즘
function fibonacci(n) {
if (n <= 1) {
return 1;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}
'텃밭 2 : FE > Algorithm' 카테고리의 다른 글
| [Algorithm] 탐욕 알고리즘과 동적 계획법 (0) | 2022.02.25 |
|---|---|
| [Algorithm] 자료구조 기초 이론 (0) | 2022.02.22 |
| [Algorithm] 고차함수 1-10 (0) | 2022.02.16 |
| [Algorithm] 재귀의 이해 (0) | 2022.01.14 |
Comments




